Набліжанага пабудова мноства Парэта ў задачы многокритериальной аптымізацыі метадам роя часціц
аўтары: Антух А. Э., Семяніхін А. С., Хасанава Р. В.
МГТУ ім. Н.Э. Баумана
ўвядзенне
У цяперашні час пры вырашэнні задач аптымізацыі ўсё больш шырокае распаўсюджанне атрымліваюць стахастычныя паводніцкія метады [1]. Адным з такіх метадаў з'яўляецца метад роя часціц (Particle Swarm Optimization, PSO), заснаваны на заканамернасцях сацыяльнага паводзінаў [2-3]. Першапачатковай мэтай даследаванняў у галіне роя часціц было выяўленне базавых прынцыпаў, дзякуючы якім зграя рыб або птушак сінхронна змяняе кірунак руху. Да цяперашняга часу канцэпцыя роя часціц развілася ў простай і перспектыўны аптымізацыйных многоагентный метад.
У метадзе PSO агентамі з'яўляюцца часціцы ў прасторы параметраў задачы аптымізацыі. У кожны момант часу (на кожнай ітэрацыі) часціцы маюць у гэтай прасторы некаторы становішча і вектар хуткасці. Для кожнага становішча часціцы вылічаецца адпаведнае значэнне мэтавай функцыі, і на гэтай аснове па пэўных правілах часціца змяняе сваё становішча і хуткасць у прасторы пошуку [3].
Дастаткова новым з'яўляецца прымяненне метаду PSO ў задачы многокритериальной аптымізацыі (Multi-Objective Swarm Optimization, MOPSO) [1]. У працы разглядаецца прымяненне гэтага метаду для набліжанага пабудовы мноства Парэта ў названай задачы.
1. Пастаноўка задачы
сукупнасць прыватных крытэрыяў аптымальнасці  утворыць вектарны крытэрыем аптымальнасці
утворыць вектарны крытэрыем аптымальнасці 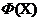 , дзе
, дзе 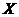 - вектар варьируемых параметраў. Але няхай будзе, што ставіцца задача мінімізацыі кожнага з прыватных крытэрыяў ў адной і той жа вобласці дапушчальных значэнняў
- вектар варьируемых параметраў. Але няхай будзе, што ставіцца задача мінімізацыі кожнага з прыватных крытэрыяў ў адной і той жа вобласці дапушчальных значэнняў 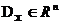 . запішам в е адачу многокритериальной аптымізацыі ў выглядзе
. запішам в е адачу многокритериальной аптымізацыі ў выглядзе
 . (1)
. (1)
Але няхай будзе, што прыватныя крытэры аптымальнасці нармалізаваныя з выкарыстаннем, напрыклад, адносных адхіленняў прыватных крытэрыяў ад іх мінімальных значэнняў:
 ,
,
дзе  ,
, 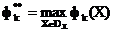 . Захаваем за нармалізаваць крытэрамі ранейшыя абазначэння.
. Захаваем за нармалізаваць крытэрамі ранейшыя абазначэння.
ўвядзем паняцце прасторы крытэрыяў  . Прастору крытэрыяў мае памернасць
. Прастору крытэрыяў мае памернасць 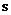 (Па ліку прыватных крытэрыяў) і ўтворыцца
(Па ліку прыватных крытэрыяў) і ўтворыцца 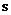 артаганальнай восямі каардынатаў, уздоўж якіх адкладаюцца значэння прыватных крытэрыяў аптымальнасці
артаганальнай восямі каардынатаў, уздоўж якіх адкладаюцца значэння прыватных крытэрыяў аптымальнасці 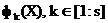 .
.
Вектарны крытэрый аптымальнасці  выконвае адлюстраванне мноства дапушчальных значэнняў
выконвае адлюстраванне мноства дапушчальных значэнняў 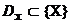 у некаторую вобласць
у некаторую вобласць 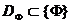 , дзе
, дзе 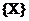 - прастору варьируемых параметраў .
- прастору варьируемых параметраў .
Ўвядзем на мностве  стаўленне перавагі
стаўленне перавагі 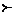 . Будзем казаць, што вектар
. Будзем казаць, што вектар 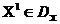 пераважней вэктару
пераважней вэктару 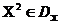 , І пісаць
, І пісаць 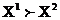 , Калі сярод роўнасцяў і няроўнасцей
, Калі сярод роўнасцяў і няроўнасцей 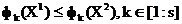 маецца хаця б адно строгае няроўнасць [4].
маецца хаця б адно строгае няроўнасць [4].
Аналагічна, на мностве ![Аналагічна, на мностве ўвядзем стаўленне дамінавання : Будзем казаць, што вектарны крытэрый аптымальнасці дамінуе вектарны крытэрый аптымальнасці , І пісаць , калі [4]](/wp-content/uploads/2019/12/be-navuka-i-adukacyu-22.gif) ўвядзем стаўленне дамінавання : Будзем казаць, што вектарны крытэрый аптымальнасці
ўвядзем стаўленне дамінавання : Будзем казаць, што вектарны крытэрый аптымальнасці 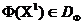 дамінуе вектарны крытэрый аптымальнасці
дамінуе вектарны крытэрый аптымальнасці 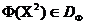 , І пісаць
, І пісаць 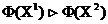 , калі
, калі 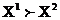 [4].
[4].
Вылучым з мноства  падмноства
падмноства 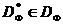 кропак, для якіх няма кропак, іх дамінуючых. Гэта мноства называецца фронтам Парэта (мал. 1). мноства
кропак, для якіх няма кропак, іх дамінуючых. Гэта мноства называецца фронтам Парэта (мал. 1). мноства 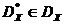 , Адпаведнае мноству
, Адпаведнае мноству 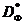 , называецца мноствам Парэта ( перагаворным мноствам , вобласцю кампрамісу ). паколькі мноства
, называецца мноствам Парэта ( перагаворным мноствам , вобласцю кампрамісу ). паколькі мноства  на малюнку 1 з'яўляецца выпуклым, то мноства
на малюнку 1 з'яўляецца выпуклым, то мноства 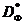 у дадзеным выпадку ўяўляе сабой дугу AB, у якой кропка A адпавядае
у дадзеным выпадку ўяўляе сабой дугу AB, у якой кропка A адпавядае 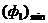 , А кропка B -
, А кропка B - 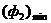 . сярод кропак
. сярод кропак 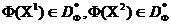 няма доминируемых, паколькі
няма доминируемых, паколькі 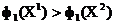 , але
, але 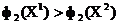 .
.

Мал. 1. Да вызначэння фронту Парэта (  )
)
Ставіцца задача набліжанага пабудовы мноства Парэта (а, тым самым, і фронту Парэта) ў задачы многокритериальной аптымізацыі (1).
2. Кананічны метад роя часціц (PSO)
Мноства часціц пазначым  , дзе
, дзе 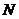 - колькасць часціц у рою (памер папуляцыі). У дыскрэтны момант часу
- колькасць часціц у рою (памер папуляцыі). У дыскрэтны момант часу 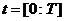 каардынаты часціцы
каардынаты часціцы 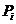 вызначаюцца вектарам
вызначаюцца вектарам 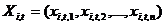 , А яе хуткасць - вектарам
, А яе хуткасць - вектарам 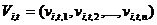 . Мноства часціц у дыскрэтны момант часу пазначым
. Мноства часціц у дыскрэтны момант часу пазначым 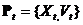 ;
; 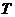 - колькасць ітэрацый. Пачатковыя каардынаты і хуткасці часціцы
- колькасць ітэрацый. Пачатковыя каардынаты і хуткасці часціцы 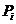 роўныя
роўныя 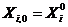 ,
, 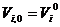 адпаведна, дзе
адпаведна, дзе 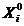 - матрыца выпадковых лікаў,
- матрыца выпадковых лікаў, 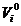 - нулявая матрыца.
- нулявая матрыца.
Ітэрацыі ў кананічным метадзе PSO выконваюцца па наступнай схеме:
 ; (2)
; (2)
 . (3)
. (3)
тут  ўяўляе сабой
ўяўляе сабой 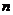 -мерный вектар псеўдавыпадковых лікаў, раўнамерна размеркаваных ў інтэрвале
-мерный вектар псеўдавыпадковых лікаў, раўнамерна размеркаваных ў інтэрвале 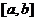 ;
; 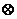 - сімвал покомпонентного множання вектараў;
- сімвал покомпонентного множання вектараў; 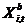 - вектар каардынатаў часціцы
- вектар каардынатаў часціцы 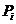 з найлепшым значэннем мэтавай функцыі
з найлепшым значэннем мэтавай функцыі 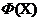 за ўвесь час пошуку
за ўвесь час пошуку 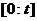 ;
; 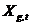 - вектар каардынатаў суседняй з дадзенай часціцы з найлепшым за час пошуку
- вектар каардынатаў суседняй з дадзенай часціцы з найлепшым за час пошуку 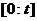 значэннем мэтавай функцыі
значэннем мэтавай функцыі 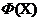 ;
; 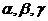 - свабодныя параметры алгарытму. Найважнейшая ў метадзе PSO паняцце суседства часціц залежыць ад выкарыстоўванай тапалогіі суседства і вызначана, напрыклад, у працы [2].
- свабодныя параметры алгарытму. Найважнейшая ў метадзе PSO паняцце суседства часціц залежыць ад выкарыстоўванай тапалогіі суседства і вызначана, напрыклад, у працы [2].
Пералік каардынатаў часціц па формулах (2), (3) можа адбывацца па сінхроннай схеме (абнаўленне каардынатаў часціц выконваецца толькі пасля вызначэння бягучых хуткасцяў ўсіх 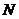 часціц) або па асінхроннай схеме (разлік новых каардынатаў часткі вырабляецца да завяршэння названых вылічэнняў).
часціц) або па асінхроннай схеме (разлік новых каардынатаў часткі вырабляецца да завяршэння названых вылічэнняў).
У працэсе ітэрацый вектар 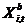 утворыць так званы уласны шлях (private guide) часціцы
утворыць так званы уласны шлях (private guide) часціцы 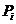 , А вектар
, А вектар 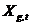 - лакальны шлях (local guide) гэтай часціцы.
- лакальны шлях (local guide) гэтай часціцы.
свабодны параметр  вызначае «інэрцыйныя» ўласцівасці часціц (пры
вызначае «інэрцыйныя» ўласцівасці часціц (пры 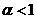 рух часціц запавольваецца). Рэкамендуемае значэнне параметру
рух часціц запавольваецца). Рэкамендуемае значэнне параметру  роўна 0,7298 [2]. У працэсе аптымізацыі можа быць эфектыўным паступовае памяншэнне каэфіцыента
роўна 0,7298 [2]. У працэсе аптымізацыі можа быць эфектыўным паступовае памяншэнне каэфіцыента  ад 0.9 да 0.4. Пры гэтым вялікія значэння параметру забяспечваюць шырокі агляд прасторы пошуку, а малыя - дакладную лакалізацыю мінімуму мэтавай функцыі. Рэкамендаваны значэння свабодных параметраў
ад 0.9 да 0.4. Пры гэтым вялікія значэння параметру забяспечваюць шырокі агляд прасторы пошуку, а малыя - дакладную лакалізацыю мінімуму мэтавай функцыі. Рэкамендаваны значэння свабодных параметраў 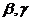 роўныя 1,49618 [2].
роўныя 1,49618 [2].
Другі кампанент у формуле (2) называецца «кагнітыўным» кампанентам (па сацыяльнай аналогіі) і фармалізуе тэндэнцыю часціцы вярнуцца ў становішча з мінімальным значэннем мэтавай функцыі. Трэці кампанент у формуле (2) называецца «сацыяльным» кампанентам. Кампанент адлюстроўвае ўплыў на дадзеную часцінку яе суседзяў.
3. Метад многокритериальной аптымізацыі роем часціц (MOPSO)
Важнай часткай метаду MOPSO з'яўляецца вызначэнне глабальна лепшай часціцы (у сэнсе формулы (1)) для кожнай часціцы ў папуляцыі. У многокритериальной задачы глабальна лепшую часціцу варта шукаць на мностве Парэта. З гэтай мэтай у метадзе MOPSO выкарыстоўваецца архіў часціц  . У ім захоўваюцца каардынаты недоминируемых часціц
. У ім захоўваюцца каардынаты недоминируемых часціц 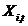 . Схема метаду MOPSO прадстаўлена на малюнку 2.
. Схема метаду MOPSO прадстаўлена на малюнку 2.
Крок 1: t = 0
Крок 2 (ініцыялізацыя):
ініцыялізацыя папуляцыі  :
:
For i = 1 to 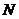
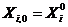 ;
; 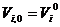 ;
; 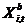 =
= 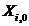
End;
Ініцыялізацыя архіва часціц:
 ;
;
Крок 3: Абнаўленне архіва часціц:  ;
;
Крок 4:
For i = 1 to 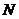
Вылічэнне вектара глабальна лепшых часціц:
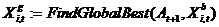 ;
;
For j = 1 to n
 ;
;
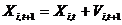
End;
If (  )
)

End;
End;
Крок 6 (праверка крытэра супыну ітэрацый):
t = t +1;
IF t  T
T
go to крок 3;
End
Мал. 2. Схема алгарытму MOPSO
У выніку працы алгарытму MOPSO на ітэрацыі  адбываецца абнаўленне архіва
адбываецца абнаўленне архіва 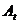 . Функцыя Update выконвае параўнанне каардынатаў часціц з архіву
. Функцыя Update выконвае параўнанне каардынатаў часціц з архіву 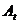 з каардынатамі часціц, атрыманымі на бягучай ітэрацыі t. Калі некаторая часціца бягучага пакалення
з каардынатамі часціц, атрыманымі на бягучай ітэрацыі t. Калі некаторая часціца бягучага пакалення 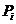 дамінуе часціцу
дамінуе часціцу 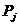 з архіву, то каардынаты часціцы
з архіву, то каардынаты часціцы 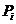 заменяя.т ў архіве каардынаты часціцы
заменяя.т ў архіве каардынаты часціцы 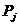 . Калі часціца
. Калі часціца 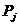 дамінуе часціцу
дамінуе часціцу 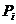 , То часціцу
, То часціцу 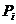 ня дадаецца ў архіў.
ня дадаецца ў архіў.
Заўважым, што з прыведзенай схемы функцыі Update вынікае, што на першай ітэрацыі, калі архіў пусты, функцыя Update дадае ў архіў ўсе часціцы бягучага пакалення, якія не дамінуюць адзін аднаго.
Выбар глабальна лепшай часціцы ажыццяўляе функцыя FindGlobalBest. Існуе некалькі спосабаў рэалізацыі гэтай функцыі. У дадзенай працы выкарыстоўваецца метад «змяняюцца» суседзяў »Х'ю і Эберхарта [5]. Разгледзім сутнасць гэтага метаду на прыкладзе задачы двухкритериальной аптымізацыі. Пошук глабальна лепшай часціцы для кожнай часціцы папуляцыі ажыццяўляецца ў гэтым выпадку наступным чынам: спачатку вылічаем адлегласць ад часціцы 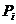 да іншых часціц архіва
да іншых часціц архіва 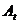 , Выкарыстоўваючы значэння першага ( «фіксаванага») крытэра аптымальнасці
, Выкарыстоўваючы значэння першага ( «фіксаванага») крытэра аптымальнасці 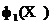 . Такім чынам, для часціцы
. Такім чынам, для часціцы 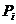 знаходзім k яе бліжэйшых лакальных суседзяў. Затым, выкарыстоўваючы другі крытэрый
знаходзім k яе бліжэйшых лакальных суседзяў. Затым, выкарыстоўваючы другі крытэрый 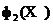 , Знаходзім найбольш аптымальную часціцу з гэтых колькасці гэтых суседзяў часціцы
, Знаходзім найбольш аптымальную часціцу з гэтых колькасці гэтых суседзяў часціцы 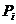 . Гэта часціца і прымаецца ў якасці глабальна лепшай часціцы для часціцы
. Гэта часціца і прымаецца ў якасці глабальна лепшай часціцы для часціцы 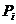 .
.
Ітэрацыі могуць працягвацца да таго часу, пакуль мноства недоминируемых рашэнняў не перастане змяняцца, альбо да дасягнення зададзенага ліку ітэрацый.
5. Даследаванне эфектыўнасці метаду MOPSO
Даследаванне выканана для наступнай тэставай задачы:
· мноства дапушчальных значэнняў
 ; (4)
; (4)
· прыватныя крытэры аптымальнасці
 (5)
(5)
Вядома, што мноства  для задачы (4), (5) мае выгляд, прадстаўлены на мал. 3б, а мноства Парэта
для задачы (4), (5) мае выгляд, прадстаўлены на мал. 3б, а мноства Парэта 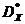 ўяўляе сабой адрэзак прамой, які злучае кропкі (0, 0), (1, 1) мал. 3а.
ўяўляе сабой адрэзак прамой, які злучае кропкі (0, 0), (1, 1) мал. 3а.
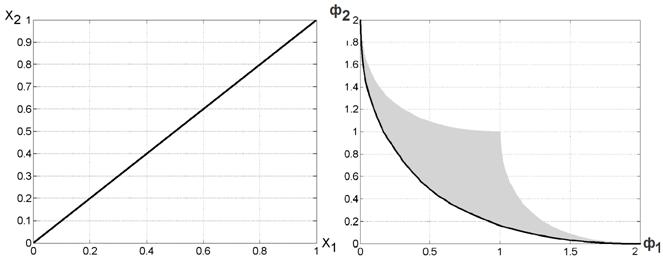
а) б)
Мал. 3. Дакладныя мноства Парэта (а) і фронт Парэта (б) для тэставай задачы
На аснове вялікай колькасці эксперыментаў было ўстаноўлена, што аптымальнымі для задачы (4), (5) з'яўляюцца наступныя параметры метаду MOPSO: памер папуляцыі  ; колькасць ітэрацый
; колькасць ітэрацый  .
.
На малюнку 4 намаляваная апраксімацыя мноства Парэта і адпаведная апраксімацыя фронту Парэта, атрыманыя для задачы (4), (5) з дапамогай алгарытму MOPSO. Атрыманне названых вынікаў запатрабавала прыкладна 10 хвілін працэсарнага часу (разлікі праводзіліся на персанальным кампутары з працэсарам 2,16 Гц і 2 ГБ опертивной памяці).

а) б)
Мал. 4. апраксімацыі мноства Парэта (а) і фронту Парэта (б) для тэставай задачы
Неабходна адзначыць, што для вылічальных простых крытэраў аптымальнасці, рашэнне задачы (1) поўным пераборам на досыць дакладнай сетцы, якая пакрывае мноства  , Патрабуе выдаткаў працэсарнага часу, параўнальных з названым вышэй часам. Аднак, пры павелічэнні складанасці крытэрыяў, метад MOPSO дазваляе знаходзіць рашэнне прымальнай дакладнасці за істотна меншы час.
, Патрабуе выдаткаў працэсарнага часу, параўнальных з названым вышэй часам. Аднак, пры павелічэнні складанасці крытэрыяў, метад MOPSO дазваляе знаходзіць рашэнне прымальнай дакладнасці за істотна меншы час.
Паколькі вядома дакладная рашэнне тэставай задачы (4), (5), маецца магчымасць колькасна ацаніць якасць атрыманай апраксімацыі мноства Парэта. Для гэтага было вылічана сярэдняе адхіленне часціцы ад ідэальнага мноства (адрэзка прамой з канцамі ў кропках (0,0), (1,1), см. Мал.3). На малюнку 5 прыведзены атрыманыя вынікі.
Суцэльнай лініяй на малюнку 5 паказана сярэдняе адхіленне ад дакладнага рашэння (M), як функцыя колькасці ітэрацый (t). Малюнак паказвае, што метад сыходзіцца ўжо на першых 100-200 ітэрацый, пасля чаго мае месца стагнацыя ітэрацыйныя працэсу.
Пункцірам на малюнку 5 паказана велічыня сярэдняга адхіленні (σ) часціц ад дакладнага рашэння. Велічыня (σ) у некаторай ступені дэманструе тое факт, што ў архіўным мностве  няма часціц, якія размешчаны суперблизко і супердалеко ад дакладнага рашэння.
няма часціц, якія размешчаны суперблизко і супердалеко ад дакладнага рашэння.
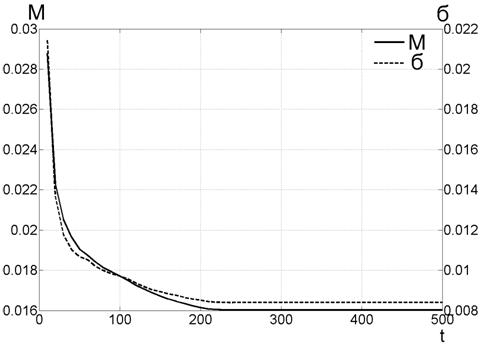
Мал. 5. Ацэнка якасці апраксімацыі
Дадаткова было выканана даследаванне прадукцыйнасці алгарытму. Для гэтага было выяўлена, якім чынам з цягам ітэрацый расце памер архіва 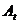 і як гэты памер ўплывае на агульны час рашэння задачы. Некаторыя вынікі эксперыментаў прыведзены на малюнку 6. На малюнку суцэльная лінія паказвае памер архіва
і як гэты памер ўплывае на агульны час рашэння задачы. Некаторыя вынікі эксперыментаў прыведзены на малюнку 6. На малюнку суцэльная лінія паказвае памер архіва 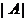 у функцыі колькасці ітэрацый (t), а пункцірнай лінія - час вылічэнняў
у функцыі колькасці ітэрацый (t), а пункцірнай лінія - час вылічэнняў 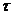 . Заўважым, што ў дадзеным варыянце алгарытму быў выкарыстаны архіў
. Заўважым, што ў дадзеным варыянце алгарытму быў выкарыстаны архіў 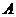 , Які не мае абмежаванні на яго памер. Гэта дазволіла назапашваць у архіве
, Які не мае абмежаванні на яго памер. Гэта дазволіла назапашваць у архіве 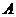 усе Парэта аптымальныя кропкі. Для рэальных задач многокритериальной аптымізацыі неабходна абмяжоўваць памер архіва, каб яго неабмежаваны рост не прывёў да недахопу памяці кампутара.
усе Парэта аптымальныя кропкі. Для рэальных задач многокритериальной аптымізацыі неабходна абмяжоўваць памер архіва, каб яго неабмежаваны рост не прывёў да недахопу памяці кампутара.
заключэнне
Праца дэманструе падыход да набліжанаму пабудове мноства Парэта ў задачы многокритериальной аптымізацыі з дапамогай метаду MOPSO. Праведзенае даследаванне паказала, што дадзены метад, быўшы адносна простым (як матэматычна, так і ў рэалізацыі), забяспечвае вырашэнне задачы з прымальнай дакладнасцю.
Мал. 6. Час вылічэнняў τ иразмер архіва  у функцыі колькасці ітэрацый
у функцыі колькасці ітэрацый 
Да недахопаў метаду можна аднесці тое, што выбар глабальна лепшай часціцы моцна залежыць ад выбару «фіксаванага» крытэра [1]. Для пераадолення гэтага недахопу плануецца выкарыстоўваць мадыфікаваныя метады, прыведзеныя, напрыклад, у артыкуле [1]. У развіццё працы плануецца таксама рэалізацыя крытэра супыну метаду, заснаванага на адсутнасці росту памеру архіва на працягу зададзенай колькасці ітэрацый.
Аўтары выказваюць падзяку Карпенка А.П. і Селиверстову Е.Ю. за плённыя абмеркавання пастаноўкі задачы і метадаў яе рашэння.
літаратура
1. Mostaghim S., Teich, J. Strategies for Finding Good Local Guides in Multi-Objective Particle Swarm Optimization (MOPSO) // Swarm Intelligence Symposium: Proceeding, 2003. - pp. 26-33.
2. Карпенка А.П., Селіверстаў Е.Ю. Глабальная аптымізацыя метадам роя часціц. Агляд // Інфармацыйныя тэхналогіі, 2010, ╧ 2, c. 25-34.
3. Субоцін С.А., Алейнік Ан.А., Алейнік Ал.А. PSO-метад, «Інтэлектуальныя мультиагентные метады (Swarm Intelligence)», ╧3, 2006, с. 55-70.
4. Карпенка А.П. Метады аптымізацыі [Электронны рэсурс] .- (http://bigor.bmstu.ru).
5. Hu X., Eberhart R. Multiobjective optimization using dynamic neighborhood particle swarm optimization // World Congress on Computational Inelligence: Proceeding, 2002.- pp. 1677-1681.