Безумоўным мінімізацыі МЕТАДЫ, метады, прызначаныя для знаходжання мінімуму функцыі многіх зменных f (х) у выпадку, калі на значэння аргументу не накладаюцца дадатковыя абмежаванні. Безумоўнай мінімізацыі метады складаюць важны клас метадаў аптымізацыі. Задача аб знаходжанні максімуму змяненнем знака функцыі f (х) зводзіцца да задачы аб знаходжанні мінімуму. У выпадку, калі f залежыць ад адной скалярнай зменнай х, мінімізацыю функцыі f (х) звычайна называюць аднамернай. Да групы метадаў аднамернай мінімізацыі адносяцца: метад палавіннага дзялення, выпадковы пошук, метад Фібаначы, метад залатога сячэння і інш.
У безумоўнай мінімізацыі метадзе ў працэсе мінімізацыі будуецца некаторая паслядоўнасць кропак х1, х2 xk шматмернага прасторы і ў залежнасці ад значэнняў функцыі f у гэтых кропках знаходзіцца новая кропка ХК + 1.Правило пабудовы паслядоўнасці вызначаецца абраным метадам мінімізацыі.
У безумоўнай мінімізацыі метадзе важную ролю адыгрывае гладкасць функцыі f. Павелічэнне гладкасці минимизируемой функцыі f дазваляе будаваць больш эфектыўныя метады. Безумоўнай мінімізацыі метады падпадзяляюць на тры асноўных класа.
рэклама
Адзін з класаў складаюць метады, не выкарыстоўвалыя вытворныя функцыі f. У гэты клас уваходзяць выпадковы пошук, метад покоординатного спуску і інш.
Іншы клас ўтвараюць градыентныя метады, у якіх мяркуецца, што функцыя f адзін раз дыферэнцыруемых. У метадзе градыентнага спуску пасля вылічэнні значэння функцыі f і яе градыенту fx ў кропцы xk новая кропка знаходзіцца па формуле
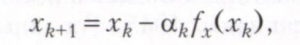
дзе αk - неадмоўнае лік (крок спуску). Пры некаторых умовах паслядоўнасць х1, х2, ... сыходзіцца да кропкі лакальнага мінімуму функцыі f (х). Калі пры кожным k велічыня αk вызначаецца з умовы аднамернай мінімізацыі функцыі f (xk + 1) па αk, то прыходзяць да метаду найхутчэйшага спуску. Існуюць таксама метады, званыя s- крокавымі, у якіх новая кропка хk вызначаецца па s папярэднім кропках. Адным з самых простых двухшагового метадаў з'яўляецца метад спалучаныя градыенту, у якім
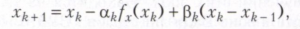
дзе αk ≥ 0, βk ≥0 - параметры, якія вызначаюцца рашэннем задачы двухмернай мінімізацыі f (xk + 1) па αk і βk.
Да трэцяга класа ставіцца метад Ньютана і яго мадыфікацыі. Мяркуецца, што функцыя f двойчы дыферэнцыруемых. Кропка xk + 1 вылічаецца па формуле
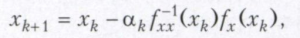
дзе f-1xx (xk) - матрыца, зваротная да матрыцы другое вытворных fxx (xk). Пры αk = 1 гэты метад называецца метадам Ньютана і часта ўжываецца пры вырашэнні прыкладных задач. Недахопам гэтага метаду з'яўляецца працаёмкасць вылічэнняў і лакальны характар збежнасці.
Існуюць мадыфікацыі метаду Ньютана. У некаторых з іх для памяншэння часу разлікаў матрыца fxx (xk) фіксуецца на некалькіх запар якія ідуць кроках. У іншых варыянтах крок αk выбіраецца з умовы мінімуму значэння функцыі f (xk + 1) альбо нормы яе градыенту.
Пералічаныя безумоўнай мінімізацыі метады прызначаныя для адшукання лакальных мінімумаў функцыі f (х), і толькі для выпуклых функцый знойдзеныя рашэнні даюць глабальны мінімум. Задача аб пошуку мінімуму яшчэ больш ўскладняецца ў выпадку адшукання ўмоўнага мінімуму, калі на значэння аргументу х накладаюцца дадатковыя абмежаванні.
Літ .: Химмельблау Д. Прыкладное нелінейнае праграмаванне. М., 1975; Еўтушэнка Ю. Г. Метады рашэння экстрэмальных задач і іх прымяненне ў сістэмах аптымізацыі. М., 1982; Паляк Б. Т. Увядзенне ў аптымізацыю. М., 1983; Васільеў Ф. П. Метады аптымізацыі. М. 2002.
Ю. Г. Еўтушэнка.