NIEKONDYCYJNE METODY MINIMALIZACJI, metody zaprojektowane w celu znalezienia minimum funkcji wielu zmiennych f (x) w przypadku, gdy dodatkowe ograniczenia nie są nakładane na wartości argumentu. Bezwarunkowe metody minimalizacji stanowią ważną klasę metod optymalizacji. Problem znalezienia maksimum poprzez zmianę znaku funkcji f (x) sprowadza się do problemu znalezienia minimum. W przypadku, gdy f zależy od pojedynczej zmiennej skalarnej x, minimalizacja funkcji f (x) jest zwykle nazywana jednowymiarową. Grupa metod minimalizacji jednowymiarowej obejmuje: pół-podział, wyszukiwanie losowe, metodę Fibonacciego, metodę złotej sekcji itp.
W metodzie bezwarunkowej minimalizacji, w procesie minimalizacji, konstruowana jest pewna sekwencja punktów x1, x2 xk przestrzeni wielowymiarowej i, w zależności od wartości funkcji f, znajduje się nowy punkt xk + 1 w tych punktach.Zasada konstruowania sekwencji jest określona przez wybraną metodę minimalizacji.
W bezwarunkowej metodzie minimalizacji istotną rolę odgrywa gładkość funkcji f. Zwiększenie gładkości zminimalizowanej funkcji f pozwala budować bardziej wydajne metody. Bezwarunkowe metody minimalizacji są podzielone na trzy główne klasy.
Reklama
Jedna klasa składa się z metod, które nie używają pochodnych funkcji f. Klasa ta obejmuje wyszukiwanie losowe, metodę spadku współrzędnych itp.
Inna klasa składa się z metod gradientowych, w których zakłada się, że funkcja f jest kiedyś różniczkowalna. W metodzie zstępującego gradientu, po obliczeniu wartości funkcji f i jej gradientu fx w punkcie xk, nowy punkt znajduje się za pomocą wzoru
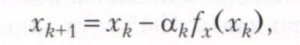
gdzie αk jest liczbą nieujemną (krok zniżania). W pewnych warunkach sekwencja x1, x2, ... zbiega się z lokalnym punktem minimalnym funkcji f (x). Jeśli dla każdego k wielkość αk jest określana na podstawie warunku jednowymiarowej minimalizacji funkcji f (xk + 1) przez αk, a następnie dochodzimy do metody najbardziej stromego zejścia. Istnieją również metody zwane s-step, w których nowy punkt xk jest określony przez poprzednie punkty. Jedną z najprostszych metod dwuetapowych jest metoda gradientu sprzężonego, w której
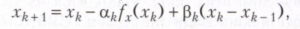
gdzie αk ≥ 0, βk ≥0 to parametry określone przez rozwiązanie problemu minimalizacji dwuwymiarowej f (xk + 1) przez αk i βk.
Trzecia klasa to metoda Newtona i jej modyfikacje. Zakłada się, że funkcja f jest dwukrotnie różniczkowalna. Punkt xk + 1 jest obliczany według wzoru
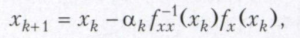
gdzie f-1xx (xk) jest macierzą odwrotną do macierzy drugich pochodnych fxx (xk). Gdy αk = 1, metoda ta nazywana jest metodą Newtona i jest często używana w rozwiązywaniu zastosowanych problemów. Wadą tej metody jest złożoność obliczeń i lokalny charakter zbieżności.
Istnieją modyfikacje metody Newtona. W niektórych z nich, w celu skrócenia czasu obliczeń, macierz fxx (xk) jest ustalana w kilku kolejnych krokach. W innych przykładach wykonania krok αk jest wybierany z warunku minimalnej wartości funkcji f (xk + 1) lub normy jej gradientu.
Wymienione metody minimalizacji bezwarunkowej mają na celu znalezienie lokalnych minimów funkcji f (x), a tylko dla funkcji wypukłych znalezione rozwiązania dają globalne minimum. Zadanie znalezienia minimum jest jeszcze bardziej skomplikowane w przypadku znalezienia warunkowego minimum, gdy dodatkowe ograniczenia są nakładane na wartości argumentu x.
Oświetlone.: Himmelblau D. Zastosowane programowanie nieliniowe. M., 1975; Evtushenko Yu G. Metody rozwiązywania ekstremalnych problemów i ich zastosowanie w systemach optymalizacji. M., 1982; Polyak B. T. Wprowadzenie do optymalizacji. M., 1983; F. P. Vasiliev Metody optymalizacji. M., 2002.
Yu G. Evtushenko.