Przybliżona konstrukcja Pareto osadzona w problemie optymalizacji wielokryterialnej metodą roju cząstek
Autorzy: Antuh A., E., Semenikhin A., S., Khasanova R. V.
MGTU je. N.E. Bauman
Wprowadzenie
Obecnie, w rozwiązywaniu problemów optymalizacyjnych, stochastyczne metody behawioralne stają się coraz bardziej rozpowszechnione [1]. Jedną z takich metod jest Particle Swarm Optimization (PSO), oparta na wzorcach zachowań społecznych [2-3]. Początkowym celem badań w dziedzinie roju cząstek było odkrycie podstawowych zasad, zgodnie z którymi stado ryb lub ptaków synchronicznie zmienia kierunek ruchu. Obecnie koncepcja roju cząstek rozwinęła się w prostą i obiecującą optymalizację wieloczynnikową.
W metodzie PSO agenty są cząstkami w przestrzeni parametrów problemu optymalizacji. W każdej chwili czasu (przy każdej iteracji) cząstki mają pewien wektor położenia i prędkości w tej przestrzeni. Dla każdej pozycji cząstki obliczana jest odpowiednia wartość funkcji celu i na tej podstawie, zgodnie z pewnymi regułami, cząstka zmienia swoją pozycję i prędkość w przestrzeni poszukiwań [3].
Zastosowanie metody PSO w optymalizacji wielu celów (Multi-Objective Swarm Optimization, MOPSO) [1] jest całkiem nowe. Artykuł omawia zastosowanie tej metody do przybliżonej konstrukcji zestawu Pareto w tym problemie.
1. Oświadczenie o problemie
Agregat kryteria częściowej optymalności 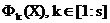 formy kryterium optymalizacji wektora
formy kryterium optymalizacji wektora 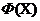 gdzie
gdzie 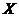 - wektor zmiennych parametrów. Załóżmy, że celem jest zminimalizowanie każdego z nich kryteria prywatne w tym samym dopuszczalny zakres
- wektor zmiennych parametrów. Załóżmy, że celem jest zminimalizowanie każdego z nich kryteria prywatne w tym samym dopuszczalny zakres 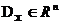 . Piszemy optymalizacja wielokryterialna w formie
. Piszemy optymalizacja wielokryterialna w formie
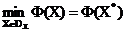 . (1)
. (1)
Zakładamy, że kryteria częściowej optymalności są znormalizowane przy użyciu, na przykład, względnych odchyleń kryteria prywatne od ich minimalnych wartości:
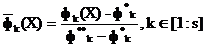 ,
,
gdzie 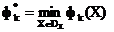 ,
, 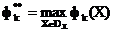 . Zachowaj normalizację kryteria to poprzedni zapis.
. Zachowaj normalizację kryteria to poprzedni zapis.
Przedstawiamy koncepcję przestrzenie kryteriów  . Przestrzeń kryteriów ma wymiar
. Przestrzeń kryteriów ma wymiar  (według liczby kryteriów prywatnych) i powstaje
(według liczby kryteriów prywatnych) i powstaje  ortogonalne osie współrzędnych, wzdłuż których deponowane są wartości kryteria częściowej optymalności
ortogonalne osie współrzędnych, wzdłuż których deponowane są wartości kryteria częściowej optymalności 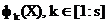 .
.
Kryterium optymalizacji wektora 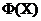 wykonuje mapowanie zestawy prawidłowych wartości
wykonuje mapowanie zestawy prawidłowych wartości  w jakimś obszarze
w jakimś obszarze  gdzie
gdzie 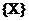 - zmienna przestrzeń parametrów .
- zmienna przestrzeń parametrów .
Przedstawiamy na planie 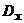 współczynnik preferencji
współczynnik preferencji 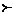 . Powiedzmy, że wektor
. Powiedzmy, że wektor 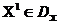 preferowany wektor
preferowany wektor 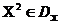 i pisz
i pisz 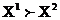 jeśli wśród równości i nierówności
jeśli wśród równości i nierówności 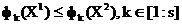 istnieje co najmniej jedna ścisła nierówność [4].
istnieje co najmniej jedna ścisła nierówność [4].
Podobnie na planie ![Podobnie na planie przedstawiamy postawa dominacji : powiemy to kryterium optymalizacji wektora zdominowany przez kryterium wektora optymalności i pisz jeśli [4]](/wp-content/uploads/2019/12/pl-nauka-i-edukacja-22.gif) przedstawiamy postawa dominacji : powiemy to kryterium optymalizacji wektora
przedstawiamy postawa dominacji : powiemy to kryterium optymalizacji wektora 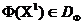 zdominowany przez kryterium wektora optymalności
zdominowany przez kryterium wektora optymalności 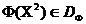 i pisz
i pisz 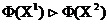 jeśli
jeśli 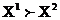 [4].
[4].
Wybierz z zestawu 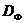 podzbiór
podzbiór 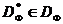 punkty, dla których nie ma punktów dominujących. Ten zestaw nazywa się frontem Pareto (rys. 1). Dużo
punkty, dla których nie ma punktów dominujących. Ten zestaw nazywa się frontem Pareto (rys. 1). Dużo 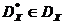 odpowiadający zestawowi
odpowiadający zestawowi 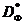 wezwał Zestaw Pareto ( zestaw negocjacyjny , obszar kompromisu ). Od wielu
wezwał Zestaw Pareto ( zestaw negocjacyjny , obszar kompromisu ). Od wielu 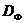 Rysunek 1 jest wypukły, a następnie zestaw
Rysunek 1 jest wypukły, a następnie zestaw 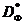 w tym przypadku jest to łuk AB, do którego odpowiada punkt A
w tym przypadku jest to łuk AB, do którego odpowiada punkt A 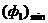 a punkt B to
a punkt B to 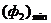 . Wśród punktów
. Wśród punktów 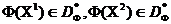 nie zdominowany, ponieważ
nie zdominowany, ponieważ 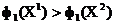 ale
ale 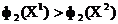 .
.
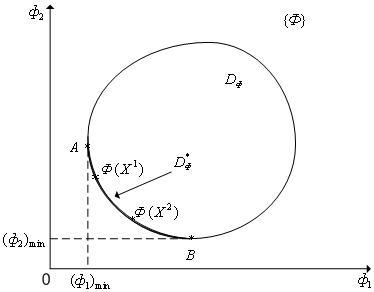
Rys. 1. Do definicji frontu Pareto ( 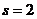 )
)
Przedstawiono problem przybliżonej konstrukcji zestawu Pareto (a tym samym frontu Pareto) w problemie optymalizacji wielokryterialnej (1).
2. Metoda roju kanonicznego ( PSO )
Wiele cząstek oznacza 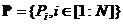 gdzie
gdzie 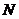 - liczba cząstek w roju (wielkość populacji). W dyskretnym momencie
- liczba cząstek w roju (wielkość populacji). W dyskretnym momencie 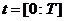 współrzędne cząstek
współrzędne cząstek  określony przez wektor
określony przez wektor 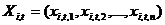 a jego prędkość jest wektorem
a jego prędkość jest wektorem 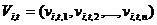 . Zbiór cząstek w dyskretnym punkcie czasu jest oznaczony przez
. Zbiór cząstek w dyskretnym punkcie czasu jest oznaczony przez 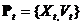 ;
; 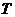 - liczba iteracji. Początkowe współrzędne i prędkości cząstki
- liczba iteracji. Początkowe współrzędne i prędkości cząstki  są równe
są równe 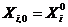 ,
, 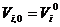 odpowiednio, gdzie
odpowiednio, gdzie 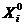 - macierz liczb losowych
- macierz liczb losowych 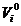 - zerowa matryca.
- zerowa matryca.
Iteracje w kanonicznej metodzie PSO są wykonywane w następujący sposób:
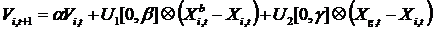 ; (2)
; (2)
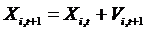 . (3)
. (3)
Tutaj 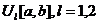 reprezentuje
reprezentuje 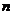 -wymiarowy wektor liczb pseudolosowych rozmieszczonych równomiernie w przedziale
-wymiarowy wektor liczb pseudolosowych rozmieszczonych równomiernie w przedziale 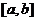 ;
; 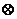 - mnożenie składowych symboli wektorów;
- mnożenie składowych symboli wektorów; 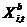 - wektor współrzędnych cząstek
- wektor współrzędnych cząstek  z najlepszą wartością funkcji celu
z najlepszą wartością funkcji celu 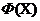 do wyszukiwania w czasie
do wyszukiwania w czasie 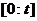 ;
; 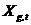 - wektor współrzędnych sąsiedniej cząstki z najlepszą podczas wyszukiwania
- wektor współrzędnych sąsiedniej cząstki z najlepszą podczas wyszukiwania 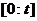 wartość funkcji celu
wartość funkcji celu 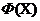 ;
; 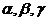 - wolne parametry algorytmu. Najważniejsza koncepcja bliskości cząstek w metodzie PSO zależy od zastosowanej topologii sąsiedztwa i została zdefiniowana na przykład w [2].
- wolne parametry algorytmu. Najważniejsza koncepcja bliskości cząstek w metodzie PSO zależy od zastosowanej topologii sąsiedztwa i została zdefiniowana na przykład w [2].
Współrzędne cząstek można przeliczyć przy użyciu wzorów (2), (3) zgodnie ze schematem synchronicznym (współrzędne cząstek są aktualizowane tylko po określeniu bieżących prędkości wszystkich 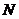 cząstki) lub schemat asynchroniczny (obliczenie nowych współrzędnych części następuje przed zakończeniem określonych obliczeń).
cząstki) lub schemat asynchroniczny (obliczenie nowych współrzędnych części następuje przed zakończeniem określonych obliczeń).
Podczas iteracji wektor 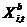 tworzy tak zwaną prywatną ścieżkę cząstki
tworzy tak zwaną prywatną ścieżkę cząstki  i wektor
i wektor 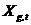 - lokalna ścieżka (lokalny przewodnik) tej cząstki.
- lokalna ścieżka (lokalny przewodnik) tej cząstki.
Bezpłatny parametr 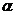 określa „inercyjne” właściwości cząstek (na
określa „inercyjne” właściwości cząstek (na 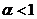 ruch cząsteczek zwalnia). Zalecana wartość
ruch cząsteczek zwalnia). Zalecana wartość 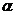 wynosi 0.7298 [2]. W procesie optymalizacji efektywny może być stopniowy spadek współczynnika.
wynosi 0.7298 [2]. W procesie optymalizacji efektywny może być stopniowy spadek współczynnika. 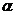 od 0,9 do 0,4. Jednocześnie duże wartości parametru zapewniają szeroki przegląd przestrzeni wyszukiwania, a małe - dokładną lokalizację minimum funkcji celu. Zalecane wolne wartości parametrów
od 0,9 do 0,4. Jednocześnie duże wartości parametru zapewniają szeroki przegląd przestrzeni wyszukiwania, a małe - dokładną lokalizację minimum funkcji celu. Zalecane wolne wartości parametrów 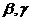 równy 1,49618 [2].
równy 1,49618 [2].
Drugi składnik we wzorze (2) nazywany jest składnikiem „poznawczym” (przez analogię społeczną) i formalizuje tendencję cząstki do powrotu do pozycji z minimalną wartością funkcji celu. Trzeci składnik we wzorze (2) nazywany jest składnikiem „społecznym”. Składnik odzwierciedla wpływ na daną cząstkę sąsiadów.
3. Metoda optymalizacji roju cząstek wielokryterialnych ( MOPSO )
Ważną częścią metody MOPSO jest określenie globalnie najlepszej cząstki (w sensie wzoru (1)) dla każdej cząstki w populacji. W przypadku problemu wielokryterialnego najlepszą globalną cząstkę należy szukać na zestawie Pareto. W tym celu archiwum cząstek jest używane w metodzie MOPSO. 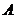 . Współrzędne nominowanych cząstek są w nim przechowywane.
. Współrzędne nominowanych cząstek są w nim przechowywane. 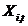 . Schemat metody MOPSO przedstawiono na rysunku 2.
. Schemat metody MOPSO przedstawiono na rysunku 2.
Krok 1: t = 0
Krok 2 (inicjalizacja):
Inicjalizacja populacji 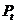 :
:
Dla i = 1 do 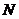
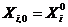 ;
; 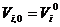 ;
; 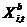 =
= 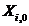
Koniec;
Inicjalizacja archiwum cząstek:
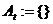 ;
;
Krok 3: Aktualizacja archiwum cząstek: 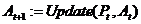 ;
;
Krok 4:
Dla i = 1 do 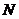
Obliczanie wektora globalnie najlepszych cząstek:
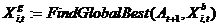 ;
;
Dla j = 1 do n
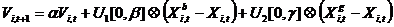 ;
;
Koniec;
Jeśli (  )
)
Koniec;
Koniec;
Krok 6 (sprawdzenie kryterium zatrzymania iteracji):
t = t + 1 ;
IF t 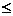 T
T
przejdź do kroku 3;
Koniec
Rys. 2. Schemat algorytmu MoPSO
W wyniku algorytmu MOPSO przy iteracji 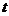 archiwum jest aktualizowane
archiwum jest aktualizowane 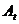 . Funkcja aktualizacji porównuje współrzędne cząstek z archiwum.
. Funkcja aktualizacji porównuje współrzędne cząstek z archiwum. 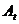 ze współrzędnymi cząstek uzyskanych przy bieżącej iteracji t . Jeśli jakieś cząstki obecnej generacji
ze współrzędnymi cząstek uzyskanych przy bieżącej iteracji t . Jeśli jakieś cząstki obecnej generacji  dominuje cząstka
dominuje cząstka 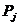 z archiwum, a następnie współrzędne cząstki
z archiwum, a następnie współrzędne cząstki  zastąpienie współrzędnych cząstek w archiwum
zastąpienie współrzędnych cząstek w archiwum 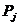 . Jeśli cząstka
. Jeśli cząstka 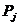 dominuje cząstka
dominuje cząstka 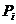 następnie cząstka
następnie cząstka 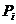 nie dodano do archiwum.
nie dodano do archiwum.
Zauważ, że funkcja Update na poniższym diagramie pokazuje, że przy pierwszej iteracji, gdy archiwum jest puste, funkcja Update dodaje do archiwum wszystkie cząstki bieżącej generacji, które się nie dominują.
Globalnie najlepsza cząstka jest wybierana przez funkcję FindGlobalBest. Istnieje kilka sposobów wdrożenia tej funkcji. W tym artykule używamy metody „zmiany” sąsiadów »Hugh i Eberharta [5]. Rozważmy istotę tej metody na przykładzie problemu dwóch kryteriów optymalizacji. Poszukiwanie globalnie najlepszej cząstki dla każdej cząstki populacji odbywa się w tym przypadku w następujący sposób: najpierw obliczamy odległość od cząstki 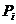 do innych cząstek archiwum
do innych cząstek archiwum 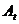 używając wartości pierwszego („stałego”) kryterium optymalności
używając wartości pierwszego („stałego”) kryterium optymalności 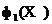 . Tak więc dla cząstki
. Tak więc dla cząstki 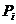 znajdź k jego najbliższych lokalnych sąsiadów. Następnie, używając drugiego kryterium
znajdź k jego najbliższych lokalnych sąsiadów. Następnie, używając drugiego kryterium 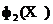 znajdujemy najbardziej optymalną cząstkę tych liczb sąsiadów
znajdujemy najbardziej optymalną cząstkę tych liczb sąsiadów 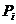 . Jest cząstką i jest akceptowana jako globalnie najlepsza cząstka dla cząstki.
. Jest cząstką i jest akceptowana jako globalnie najlepsza cząstka dla cząstki. 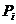 .
.
Iteracje mogą być kontynuowane, aż zestaw niezdominowanych rozwiązań przestanie się zmieniać lub do momentu osiągnięcia określonej liczby iteracji.
5. Badanie skuteczności metody MOPSO
Badanie przeprowadzono dla następującego zadania testowego:
· zestaw prawidłowych wartości
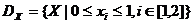 ; (4)
; (4)
· kryteria częściowej optymalności
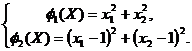 (5)
(5)
Wiadomo, że wielu 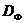 dla problemu (4), (5) ma postać pokazaną na rys. 3b, i Zestaw Pareto
dla problemu (4), (5) ma postać pokazaną na rys. 3b, i Zestaw Pareto 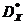 to segment linii łączący punkty (0, 0), (1, 1) rys. 3a
to segment linii łączący punkty (0, 0), (1, 1) rys. 3a
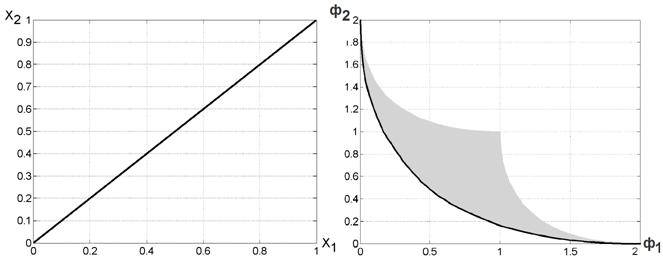
a) b)
Rys. 3. Dokładny zestaw Pareto (a) i przód Pareto (b) dla problemu testowego
Na podstawie dużej liczby eksperymentów stwierdzono, że następujące parametry metody MOPSO są optymalne dla problemu (4), (5): wielkość populacji  ; liczba iteracji
; liczba iteracji  .
.
Rysunek 4 przedstawia przybliżenie zestawu Pareto i odpowiadające mu przybliżenie frontu Pareto, uzyskane dla problemu (4), (5) przy użyciu algorytmu MOPSO. Uzyskanie tych wyników zajęło około 10 minut czasu procesora (obliczenia przeprowadzono na komputerze osobistym z procesorem 2,16 Hz i 2 GB pamięci operacyjnej).
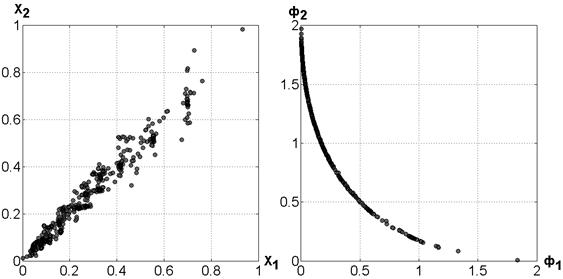
a) b)
Rys. 4. Przybliżenie zestawu Pareto (a) i przodu Pareto (b) dla problemu testowego
Należy zauważyć, że w przypadku prostych obliczeniowo kryteriów optymalności rozwiązaniem problemu (1) jest pełne wyczerpujące wyszukiwanie w wystarczająco dokładnej siatce obejmującej zestaw 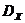 , wymaga czasu procesora porównywalnego z powyższym czasem. Jednak wraz ze wzrostem złożoności kryteriów metoda MOPSO umożliwia znalezienie rozwiązania o akceptowalnej dokładności w znacznie krótszym czasie.
, wymaga czasu procesora porównywalnego z powyższym czasem. Jednak wraz ze wzrostem złożoności kryteriów metoda MOPSO umożliwia znalezienie rozwiązania o akceptowalnej dokładności w znacznie krótszym czasie.
Ponieważ znamy dokładne rozwiązanie problemu testowego (4), (5), możliwe jest określenie jakości uzyskanego przybliżenia zestawu Pareto. W tym celu obliczono średnie odchylenie cząstki od idealnego zestawu (odcinek linii prostej z końcami w punktach (0,0), (1,1), patrz rys. 3a). Rysunek 5 przedstawia uzyskane wyniki.
Linia ciągła na rysunku 5 pokazuje średnie odchylenie od dokładnego roztworu ( M ), jako funkcję liczby iteracji ( t ). Rysunek pokazuje, że metoda zbiega się już przy pierwszych 100-200 iteracjach, po których następuje stagnacja procesu iteracyjnego.
Linia przerywana na rysunku 5 pokazuje średnie odchylenie (σ) cząstek od dokładnego roztworu. Wartość (σ) w pewnym stopniu pokazuje, że w zestawie archiwum 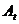 Nie ma cząstek, które są bardzo bliskie i dalekie od dokładnego rozwiązania.
Nie ma cząstek, które są bardzo bliskie i dalekie od dokładnego rozwiązania.
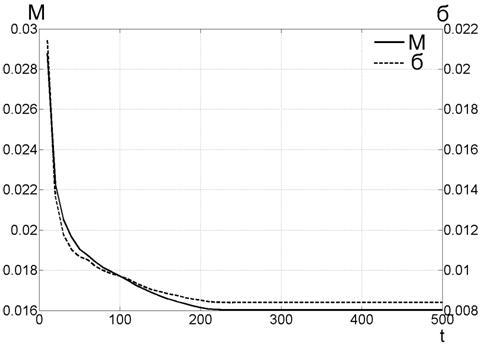
Rys. 5. Ocena jakości zbliżenia
Dodatkowo przeprowadzono badanie wydajności algorytmu. W tym celu ujawniono, w jaki sposób rozmiar archiwum rośnie wraz z przebiegiem iteracji. 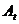 i jak ten rozmiar wpływa na całkowity czas rozwiązania problemu. Niektóre wyniki eksperymentalne pokazano na rysunku 6. Na rysunku linia ciągła pokazuje rozmiar archiwum.
i jak ten rozmiar wpływa na całkowity czas rozwiązania problemu. Niektóre wyniki eksperymentalne pokazano na rysunku 6. Na rysunku linia ciągła pokazuje rozmiar archiwum. 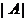 jako funkcja liczby iteracji ( t ), a linia przerywana jest czasem obliczeń
jako funkcja liczby iteracji ( t ), a linia przerywana jest czasem obliczeń 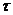 . Zauważ, że w tej wersji algorytmu użyto archiwum
. Zauważ, że w tej wersji algorytmu użyto archiwum 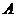 nie ograniczony rozmiar. Pozwoliło to zgromadzić się w archiwum
nie ograniczony rozmiar. Pozwoliło to zgromadzić się w archiwum 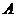 wszystkie optymalne punkty Pareto. W przypadku rzeczywistych zadań optymalizacji wielokryterialnej konieczne jest ograniczenie rozmiaru archiwum, aby jego nieograniczony wzrost nie prowadził do braku pamięci komputera.
wszystkie optymalne punkty Pareto. W przypadku rzeczywistych zadań optymalizacji wielokryterialnej konieczne jest ograniczenie rozmiaru archiwum, aby jego nieograniczony wzrost nie prowadził do braku pamięci komputera.
Wniosek
Praca demonstruje podejście do przybliżonej konstrukcji zestawu Pareto w problemie optymalizacji wielokryterialnej przy użyciu metody MOPSO. Badanie wykazało, że metoda ta, stosunkowo prosta (zarówno matematycznie, jak i implementacyjna), zapewnia rozwiązanie problemu z akceptowalną dokładnością.
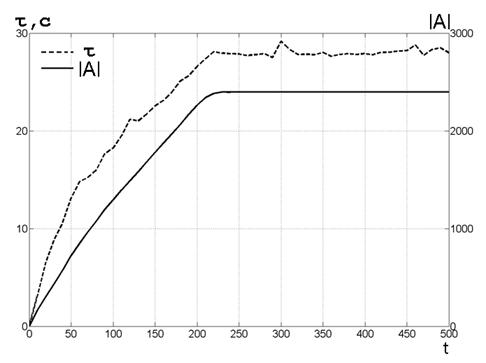
Rys. 6. Czas obliczeniowy τ i rozmiar archiwum  jako funkcja liczby iteracji
jako funkcja liczby iteracji 
Wady tej metody obejmują fakt, że wybór globalnie najlepszej cząstki silnie zależy od wyboru „stałego” kryterium [1]. Aby przezwyciężyć tę wadę, planuje się zastosowanie zmodyfikowanych metod podanych na przykład w artykule [1]. Podczas opracowywania pracy planowane jest również wdrożenie kryterium zatrzymania metody w oparciu o brak wzrostu rozmiaru archiwum dla danej liczby iteracji.
Autorzy są wdzięczni Karpenko A.P. i Seliverstovu E.Yu. za owocne dyskusje na temat problemu i metod jego rozwiązania.
Literatura
1. Mostaghim S., Teich, Multi-Objective Particle Swarm Optimization (MOPSO); J. Swiss Intelligence Symposium: Proceeding, 2003. - str. 26–33.
2. Karpenko A.P., Seliverstov E.Yu. Globalna optymalizacja przez rój cząstek. Przegląd // Information Technologies, 2010, 2, s. 25-34.
3. Subbotin SA, Oleinik An.A., Oleinik Al.A. Metoda PSO, „Inteligentne metody wieloagentowe (Swarm Intelligence)”, 3, 2006, s. 55-70.
4. Karpenko A.P. Metody optymalizacji [Zasób elektroniczny] .- (http://bigor.bmstu.ru).
5. Hu X., Eberhart R. Optymalizacja wielokryterialna z wykorzystaniem optymalizacji dynamicznego roju cząstek // Światowy kongres na temat obliczeniowej inteligencji: Proceeding, 2002.- str. 1677-1681.