БЕЗУМОВНОГО МІНІМІЗАЦІЇ МЕТОДИ, методи, призначені для знаходження мінімуму функції багатьох змінних f (х) в разі, коли на значення аргументу не накладаються додаткові обмеження. Безумовної мінімізації методи складають важливий клас методів оптимізації. Завдання про знаходження максимуму зміною знака функції f (х) зводиться до задачі про знаходження мінімуму. У разі, коли f залежить від однієї скалярної змінної х, мінімізацію функції f (х) зазвичай називають одновимірної. До групи методів одновимірної мінімізації відносяться: метод половинного ділення, випадковий пошук, метод Фібоначчі, метод золотого перерізу та ін.
У безумовної мінімізації методі в процесі мінімізації будується деяка послідовність точок х1, х2 xk багатовимірного простору і в залежності від значень функції f в цих точках знаходиться нова точка хк + 1.Правило побудови послідовності визначається обраним методом мінімізації.
У безумовної мінімізації методі важливу роль відіграє гладкість функції f. Збільшення гладкості функції, що мінімізується f дозволяє будувати більш ефективні методи. Безумовної мінімізації методи підрозділяють на три основні класи.
Реклама
Один з класів складають методи, які не використовують похідні функції f. У цей клас входять випадковий пошук, метод покоордінатного спуску і ін.
Інший клас утворюють градієнтні методи, в яких передбачається, що функція f один раз дифференцируема. У методі градієнтного спуску після обчислення значення функції f і її градієнта fx в точці xk нова точка знаходиться по формулі
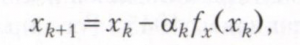
де αk - невід'ємне число (крок спуску). При деяких умовах послідовність х1, х2, ... сходиться до точки локального мінімуму функції f (х). Якщо при кожному k величина αk визначається з умови одновимірної мінімізації функції f (xk + 1) по αk, то приходять до методу найшвидшого спуску. Існують також методи, звані s- кроковими, в яких нова точка хk визначається по s попереднім точкам. Одним з найпростіших двокрокового методів є метод сполученого градієнта, в якому
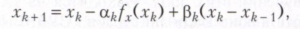
де αk ≥ 0, βk ≥0 - параметри, які визначаються рішенням завдання двовимірної мінімізації f (xk + 1) по αk і βk.
До третього класу належить метод Ньютона і його модифікації. Передбачається, що функція f двічі диференційована. Точка xk + 1 обчислюється за формулою
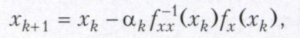
де f-1xx (xk) - матриця, обернена до матриці других похідних fxx (xk). При αk = 1 цей метод називається методом Ньютона і часто застосовується при вирішенні прикладних задач. Недоліком цього методу є трудомісткість обчислень і локальний характер збіжності.
Існують модифікації методу Ньютона. У деяких з них для зменшення часу розрахунків матриця fxx (xk) фіксується на кількох поспіль кроках. В інших варіантах крок αk вибирається з умови мінімуму значення функції f (xk + 1) або норми її градієнта.
Перераховані безумовної мінімізації методи призначені для відшукання локальних мінімумів функції f (х), і тільки для опуклих функцій знайдені рішення дають глобальний мінімум. Завдання про пошук мінімуму ще більш ускладнюється в разі відшукання умовного мінімуму, коли на значення аргументу х накладаються додаткові обмеження.
Літ .: Гіммельблау Д. Прикладне нелінійне програмування. М., 1975; Євтушенко Ю. Г. Методи розв'язування екстремальних завдань і їх застосування в системах оптимізації. М., 1982; Поляк Б. Т. Введення в оптимізацію. М., 1983; Васильєв Ф. П. Методи оптимізації. , 2002.
Ю. Г. Євтушенко.