Наближене побудова безлічі парето в завданню багатокритеріальної оптимізації методом рою частинок
автори: Антух А. Е., Семеніхін А. С., Хасанова Р. В.
МГТУ ім. Н.е. Баумана
Вступ
В даний час при вирішенні завдань оптимізації все більш широке поширення набувають стохастичні поведінкові методи [1]. Одним з таких методів є метод рою частинок (Particle Swarm Optimization, PSO), заснований на закономірностях соціальної поведінки [2-3]. Первинною метою досліджень в області рою частинок було виявлення базових принципів, завдяки яким зграя риб або птахів синхронно змінює напрямок руху. До теперішнього часу концепція рою частинок розвинулася в простий і перспективний оптимізаційний багатоагентного метод.
У методі PSO агентами є частки в просторі параметрів задачі оптимізації. У кожен момент часу (на кожній ітерації) частки мають в цьому просторі деякий стан і вектор швидкості. Для кожного положення частинки обчислюється відповідне значення цільової функції, і на цій основі за певними правилами частка змінює своє положення і швидкість в просторі пошуку [3].
Досить новим є застосування методу PSO в завданню багатокритеріальної оптимізації (Multi-Objective Swarm Optimization, MOPSO) [1]. В роботі розглядається застосування цього методу для наближеного побудови безлічі Парето у зазначеній задачі.
1. Постановка завдання
сукупність приватних критеріїв оптимальності 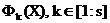 утворює векторний критерієм оптимальності
утворює векторний критерієм оптимальності 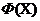 , де
, де 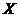 - вектор змінних параметрів. Покладемо, що ставиться завдання мінімізації кожного з приватних критеріїв в одній і тій же області допустимих значень
- вектор змінних параметрів. Покладемо, що ставиться завдання мінімізації кожного з приватних критеріїв в одній і тій же області допустимих значень 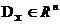 . запишемо з Адачі багатокритеріальної оптимізації у вигляді
. запишемо з Адачі багатокритеріальної оптимізації у вигляді
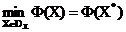 . (1)
. (1)
Покладемо, що приватні критерії оптимальності нормалізовані з використанням, наприклад, відносних відхилень приватних критеріїв від їх мінімальних значень:
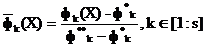 ,
,
де 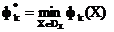 ,
, 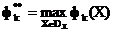 . Збережемо за нормалізованими критеріями колишні позначення.
. Збережемо за нормалізованими критеріями колишні позначення.
введемо поняття простору критеріїв 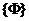 . Простір критеріїв має розмірність
. Простір критеріїв має розмірність 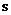 (По числу приватних критеріїв) і утворюється
(По числу приватних критеріїв) і утворюється 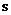 ортогональними осями координат, уздовж яких відкладаються значення приватних критеріїв оптимальності
ортогональними осями координат, уздовж яких відкладаються значення приватних критеріїв оптимальності 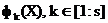 .
.
Векторний критерій оптимальності 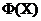 виконує відображення безлічі допустимих значень
виконує відображення безлічі допустимих значень 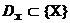 в деяку область
в деяку область 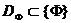 , де
, де 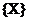 - простір змінних параметрів .
- простір змінних параметрів .
Введемо на безлічі 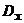 відношення переваги
відношення переваги 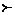 . Будемо говорити, що вектор
. Будемо говорити, що вектор 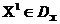 краще вектора
краще вектора 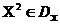 , і писати
, і писати 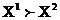 , Якщо серед рівностей і нерівностей
, Якщо серед рівностей і нерівностей 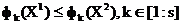 є хоча б одне суворе нерівність [4].
є хоча б одне суворе нерівність [4].
Аналогічно, на безлічі ![Аналогічно, на безлічі введемо відношення домінування : Будемо говорити, що векторний критерій оптимальності домінує векторний критерій оптимальності , і писати , якщо [4]](/wp-content/uploads/2019/12/uk-nauka-ta-osvita-22.gif) введемо відношення домінування : Будемо говорити, що векторний критерій оптимальності
введемо відношення домінування : Будемо говорити, що векторний критерій оптимальності 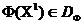 домінує векторний критерій оптимальності
домінує векторний критерій оптимальності 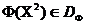 , і писати
, і писати 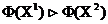 , якщо
, якщо 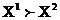 [4].
[4].
Виділимо з безлічі 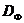 підмножина
підмножина 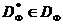 точок, для яких немає точок, їх домінуючих. Це безліч називається фронтом Парето (рис. 1). безліч
точок, для яких немає точок, їх домінуючих. Це безліч називається фронтом Парето (рис. 1). безліч 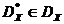 , Відповідне безлічі
, Відповідне безлічі 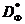 , називається безліччю Парето ( переговорним безліччю , областю компромісу ). оскільки безліч
, називається безліччю Парето ( переговорним безліччю , областю компромісу ). оскільки безліч 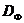 на малюнку 1 є опуклим, то безліч
на малюнку 1 є опуклим, то безліч 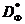 в даному випадку є дугу AB, в якій точка A відповідає
в даному випадку є дугу AB, в якій точка A відповідає 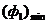 , А точка B -
, А точка B - 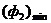 . серед точок
. серед точок 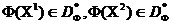 немає домінованих, оскільки
немає домінованих, оскільки 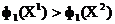 , але
, але 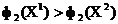 .
.
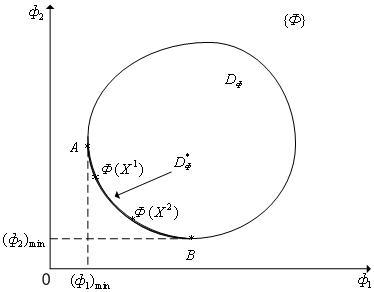
Мал. 1. До визначення фронту Парето ( 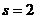 )
)
Ставиться завдання наближеного побудови безлічі Парето (а, тим самим, і фронту Парето) в задачі багатокритеріальної оптимізації (1).
2. Канонічний метод рою частинок (PSO)
Безліч частинок позначимо 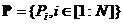 , де
, де 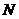 - кількість частинок в рої (розмір популяції). У дискретний момент часу
- кількість частинок в рої (розмір популяції). У дискретний момент часу 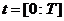 координати частинки
координати частинки  визначаються вектором
визначаються вектором 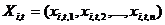 , А її швидкість - вектором
, А її швидкість - вектором 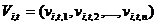 . Безліч частинок в дискретний момент часу позначимо
. Безліч частинок в дискретний момент часу позначимо 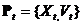 ;
; 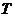 - кількість ітерацій. Початкові координати і швидкості частки
- кількість ітерацій. Початкові координати і швидкості частки  рівні
рівні 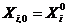 ,
, 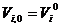 відповідно, де
відповідно, де 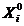 - матриця випадкових чисел,
- матриця випадкових чисел, 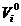 - нульова матриця.
- нульова матриця.
Ітерації в канонічному методі PSO виконуються за наступною схемою:
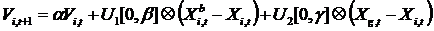 ; (2)
; (2)
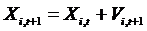 . (3)
. (3)
тут 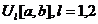 являє собою
являє собою 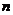 -мірний вектор псевдовипадкових чисел, рівномірно розподілених в інтервалі
-мірний вектор псевдовипадкових чисел, рівномірно розподілених в інтервалі 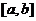 ;
; 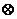 - символ покомпонентного множення векторів;
- символ покомпонентного множення векторів; 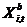 - вектор координат частинки
- вектор координат частинки  з найкращим значенням цільової функції
з найкращим значенням цільової функції 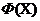 за весь час пошуку
за весь час пошуку 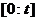 ;
; 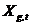 - вектор координат сусідній з даної частинки з найкращим за час пошуку
- вектор координат сусідній з даної частинки з найкращим за час пошуку 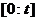 значенням цільової функції
значенням цільової функції 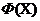 ;
; 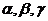 - вільні параметри алгоритму. Найважливіше в методі PSO поняття сусідства частинок залежить від використовуваної топології сусідства і визначено, наприклад, в роботі [2].
- вільні параметри алгоритму. Найважливіше в методі PSO поняття сусідства частинок залежить від використовуваної топології сусідства і визначено, наприклад, в роботі [2].
Перерахунок координат частинок за формулами (2), (3) може відбуватися по синхронної схемою (оновлення координат частинок виконується тільки після визначення поточних швидкостей всіх 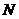 частинок) або по асинхронної схемою (розрахунок нових координат частини проводиться до завершення зазначених обчислень).
частинок) або по асинхронної схемою (розрахунок нових координат частини проводиться до завершення зазначених обчислень).
В процесі ітерацій вектор 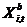 утворює так званий власний шлях (private guide) частки
утворює так званий власний шлях (private guide) частки  , А вектор
, А вектор 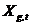 - локальний шлях (local guide) цієї частки.
- локальний шлях (local guide) цієї частки.
вільний параметр 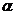 визначає «інерційні» властивості частинок (при
визначає «інерційні» властивості частинок (при 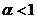 рух частинок сповільнюється). Рекомендоване значення параметра
рух частинок сповільнюється). Рекомендоване значення параметра 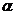 одно 0,7298 [2]. В процесі оптимізації може бути ефективним поступове зменшення коефіцієнта
одно 0,7298 [2]. В процесі оптимізації може бути ефективним поступове зменшення коефіцієнта 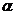 від 0.9 до 0.4. При цьому великі значення параметра забезпечують широкий огляд простору пошуку, а малі - точну локалізацію мінімуму цільової функції. Рекомендовані значення вільних параметрів
від 0.9 до 0.4. При цьому великі значення параметра забезпечують широкий огляд простору пошуку, а малі - точну локалізацію мінімуму цільової функції. Рекомендовані значення вільних параметрів 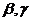 рівні 1,49618 [2].
рівні 1,49618 [2].
Другий компонент у формулі (2) називається «когнітивним» компонентом (щодо соціального аналогії) і формалізує тенденцію частки повернутися в стан з мінімальним значенням цільової функції. Третій компонент у формулі (2) називається «соціальним» компонентом. Компонент відображає вплив на дану частку її сусідів.
3. Метод багатокритеріальної оптимізації роєм часток (MOPSO)
Важливою частиною методу MOPSO є визначення глобально кращої частки (в сенсі формули (1)) для кожної частки в популяції. У многокритериальной завданню глобально кращу частку слід шукати на множині Парето. З цією метою в методі MOPSO використовується архів частинок 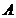 . У ньому зберігаються координати недомініруемих частинок
. У ньому зберігаються координати недомініруемих частинок 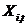 . Схема методу MOPSO представлена на малюнку 2.
. Схема методу MOPSO представлена на малюнку 2.
Крок 1: t = 0
Крок 2 (ініціалізація):
ініціалізація популяції 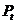 :
:
For i = 1 to 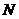
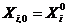 ;
; 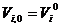 ;
; 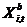 =
= 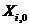
End;
Ініціалізація архіву частинок:
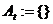 ;
;
Крок 3: Оновлення архіву частинок: 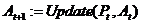 ;
;
Крок 4:
For i = 1 to 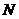
Обчислення вектора глобально кращих частинок:
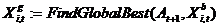 ;
;
For j = 1 to n
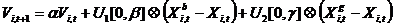 ;
;
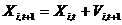
End;
If ( 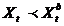 )
)
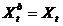
End;
End;
Крок 6 (перевірка критерію зупину ітерацій):
t = t +1;
IF t 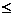 T
T
go to крок 3;
End
Мал. 2. Схема алгоритму MOPSO
В результаті роботи алгоритму MOPSO на ітерації 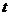 відбувається оновлення архіву
відбувається оновлення архіву 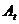 . Функція Update виконує порівняння координат частинок з архіву
. Функція Update виконує порівняння координат частинок з архіву 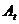 з координатами частинок, отриманими на поточній ітерації t. Якщо деяка частка поточного покоління
з координатами частинок, отриманими на поточній ітерації t. Якщо деяка частка поточного покоління  домінує частку
домінує частку 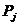 з архіву, то координати частинки
з архіву, то координати частинки  заменяя.т в архіві координати частинки
заменяя.т в архіві координати частинки 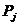 . якщо частка
. якщо частка 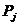 домінує частку
домінує частку 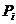 , То частку
, То частку 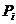 Не додає до архіву.
Не додає до архіву.
Зауважимо, що з наведеної схеми функції Update слід, що на першій ітерації, коли архів порожній, функція Update додає до архіву всі частинки поточного покоління, які не домінують один одного.
Вибір глобально кращої частки здійснює функція FindGlobalBest. Існує кілька способів реалізації цієї функції. У даній роботі використовується метод «мінливих» сусідів »Х'ю і Еберхарта [5]. Розглянемо суть цього методу на прикладі завдання двухкрітеріальной оптимізації. Пошук глобально кращої частки для кожної частки популяції здійснюється в цьому випадку наступним чином: спочатку обчислюємо відстань від частки 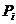 до інших частинок архіву
до інших частинок архіву 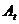 , Використовуючи значення першого ( «фіксованого») критерію оптимальності
, Використовуючи значення першого ( «фіксованого») критерію оптимальності 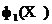 . Таким чином, для частинки
. Таким чином, для частинки 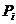 знаходимо k її найближчих локальних сусідів. Потім, використовуючи другий критерій
знаходимо k її найближчих локальних сусідів. Потім, використовуючи другий критерій 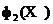 , Знаходимо найбільш оптимальну частку з цих числа цих сусідів частки
, Знаходимо найбільш оптимальну частку з цих числа цих сусідів частки 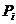 . Це частинка і приймається як глобальна кращої частки для частинки
. Це частинка і приймається як глобальна кращої частки для частинки 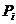 .
.
Ітерації можуть тривати до тих пір, поки безліч недомініруемих рішень не перестане змінюватися, або до досягнення заданого числа ітерацій.
5. Дослідження ефективності методу MOPSO
Дослідження виконано для наступної тестової задачі:
· безліч допустимих значень
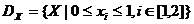 ; (4)
; (4)
· приватні критерії оптимальності
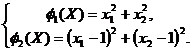 (5)
(5)
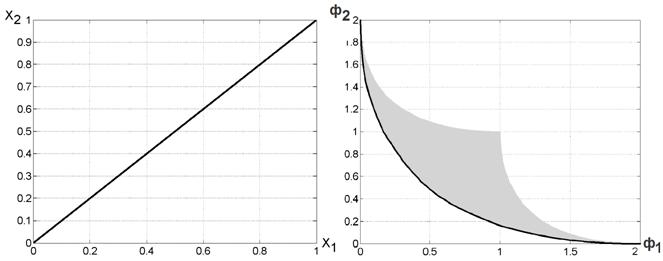
Відомо, що безліч 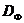 для завдання (4), (5) має вигляд, представлені на рис. 3б, а безліч Парето
для завдання (4), (5) має вигляд, представлені на рис. 3б, а безліч Парето 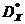 являє собою відрізок прямої, що з'єднує точки (0, 0), (1, 1) рис. 3а.
являє собою відрізок прямої, що з'єднує точки (0, 0), (1, 1) рис. 3а.
а) б)
Мал. 3. Точні безліч Парето (а) і фронт Парето (б) для тестового завдання
На основі великої кількості експериментів було встановлено, що оптимальними для завдання (4), (5) є наступні параметри методу MOPSO: розмір популяції 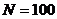 ; кількість ітерацій
; кількість ітерацій 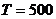 .
.
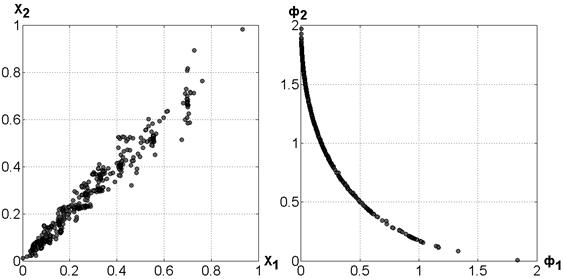
На малюнку 4 зображено апроксимація безлічі Парето і відповідна апроксимація фронту Парето, отримані для завдання (4), (5) за допомогою алгоритму MOPSO. Отримання зазначених результатів зажадало приблизно 10 хвилин процесорного часу (розрахунки проводилися на персональному комп'ютері з процесором 2,16 Гц і 2 ГБ опертівной пам'яті).
а) б)
Мал. 4. Апроксимація безлічі Парето (а) і фронту Парето (б) для тестового завдання
Необхідно відзначити, що для обчислювально простих критеріїв оптимальності, рішення задачі (1) повним перебором на досить точної сітці, що покриває безліч  , Вимагає витрат процесорного часу, порівнянних із зазначеним вище часом. Однак, при збільшенні складності критеріїв, метод MOPSO дозволяє знаходити рішення прийнятної точності за суттєво менший час.
, Вимагає витрат процесорного часу, порівнянних із зазначеним вище часом. Однак, при збільшенні складності критеріїв, метод MOPSO дозволяє знаходити рішення прийнятної точності за суттєво менший час.
Оскільки відомо точне рішення тестового завдання (4), (5), є можливість кількісно оцінити якість отриманої апроксимації безлічі Парето. Для цього було обчислено середнє відхилення частки від ідеального безлічі (відрізка прямої з кінцями в точках (0,0), (1,1), див. Рис.3). На малюнку 5 наведено отримані результати.
Суцільною лінією на малюнку 5 показано середнє відхилення від точного рішення (M), як функція числа ітерацій (t). Малюнок показує, що метод сходиться вже на перших 100-200 ітераціях, після чого має місце стагнація ітераційного процесу.
Пунктиром на малюнку 5 показана величина середнього відхилення (σ) частинок від точного рішення. Величина (σ) в деякій мірі демонструє те факт, що в архівному безлічі  немає частинок, які розташовані суперблізко і супердалеко від точного рішення.
немає частинок, які розташовані суперблізко і супердалеко від точного рішення.
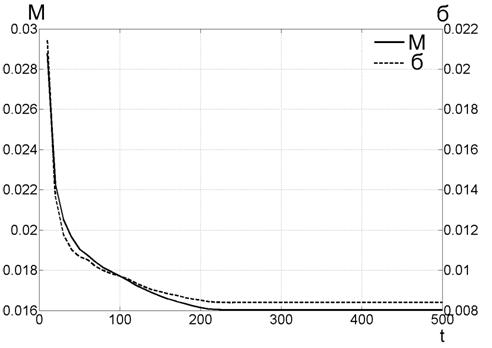
Мал. 5. Оцінка якості апроксимації
Додатково було виконано дослідження продуктивності алгоритму. Для цього було виявлено, яким чином з плином ітерацій зростає розмір архіву  і як цей розмір впливає на загальний час виконання завдання. Деякі результати експериментів наведені на малюнку 6. На малюнку суцільна лінія показує розмір архіву
і як цей розмір впливає на загальний час виконання завдання. Деякі результати експериментів наведені на малюнку 6. На малюнку суцільна лінія показує розмір архіву 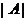 в функції кількості ітерацій (t), а пунктирна лінія - час обчислень
в функції кількості ітерацій (t), а пунктирна лінія - час обчислень 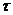 . Зауважимо, що в даному варіанті алгоритму був використаний архів
. Зауважимо, що в даному варіанті алгоритму був використаний архів 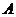 , Який не має обмеження на його розмір. Це дозволило накопичувати в архіві
, Який не має обмеження на його розмір. Це дозволило накопичувати в архіві 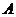 всі Парето оптимальні точки. Для реальних задач багатокритеріальної оптимізації необхідно обмежувати розмір архіву, щоб його необмежений зростання не призвело до нестачі пам'яті комп'ютера.
всі Парето оптимальні точки. Для реальних задач багатокритеріальної оптимізації необхідно обмежувати розмір архіву, щоб його необмежений зростання не призвело до нестачі пам'яті комп'ютера.
висновок
Робота демонструє підхід до наближеного побудови безлічі Парето в завданню багатокритеріальної оптимізації за допомогою методу MOPSO. Проведене дослідження показало, що даний метод, будучи відносно простим (як математично, так і в реалізації), забезпечує вирішення завдання з прийнятною точністю.
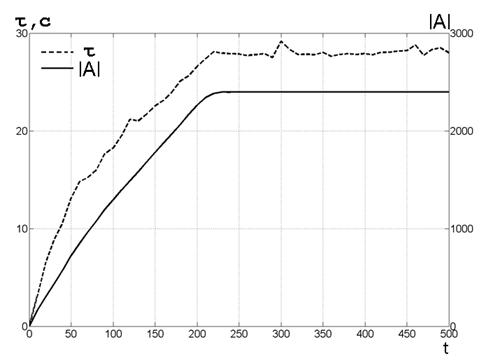
Мал. 6. Час обчислень τ іразмер архіву 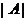 в функції кількості ітерацій
в функції кількості ітерацій 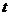
До недоліків методу можна віднести те, що вибір глобально кращої частки сильно залежить від вибору «фіксованого» критерію [1]. Для подолання цього недоліку планується використовувати модифіковані методи, наведені, наприклад, в статті [1]. У розвиток роботи планується також реалізація критерію зупину методу, заснованого на відсутності зростання розміру архіву протягом заданої кількості ітерацій.
Автори висловлюють подяку Карпенко А.П. і Селіверстова Є.Ю. за плідні обговорення постановки задачі і методів її вирішення.
література
1. Mostaghim S., Teich, J. Strategies for Finding Good Local Guides in Multi-Objective Particle Swarm Optimization (MOPSO) // Swarm Intelligence Symposium: Proceeding, 2003. - pp. 26-33.
2. Карпенко А.П., Селіверстов Є.Ю. Глобальна оптимізація методом рою частинок. Огляд // Інформаційні технології, 2010 ╧ 2, c. 25-34.
3. Суботін С.О., Олійник Ан.А., Олійник Ал.А. PSO-метод, «Інтелектуальні мультиагентні методи (Swarm Intelligence)», ╧3, 2006, с. 55-70.
4. Карпенко А.П. Методи оптимізації [Електронний ресурс] .- (http://bigor.bmstu.ru).
5. Hu X., Eberhart R. Multiobjective optimization using dynamic neighborhood particle swarm optimization // World Congress on Computational Inelligence: Proceeding, 2002.- pp. 1677-1681.